数据结构初步

前言

数据结构的设计思路来源于程序设计中的各种基本算法思想，同时又对进一步研究和实现更加深入的算法提供的工具技术，此篇文章旨在探讨一些基础的线性数据结构和树形数据结构。

正文

哈希

哈希表

哈希表与离散化思想类似，可以用 Hash 函数把一系列复杂的信息映射到一个容易维护的值域内。
Hash 表主要包含两个基本操作：

1. 计算 Hash 函数的值；
2. 定位到对应链表中依次遍历、比较。
   当 Hash 函数设计较好时，原始信息会被比较均匀地分配到各个表头之后。若原始信息总数与表头数组长度都是 O(N) 级别且 Hash 函数分散均匀，几乎不产生冲突，那么查找、统计地时间复杂度期望为 O(1)。
   下面我们来介绍 Hash 表的做法：
   设计 Hash 函数为 H(x) = (x mod P) + 1，其中 P 是一个比较大的质数，但不超过 N。显然，这个Hash函数把数列 A 分为 P 类，我们可以一次考虑数列中的每个数 A[i]，定位到 head[H(A[i])] 这个表头所指向的链表。如果该链表中不包含 A[i]，我们就在表头后插入一个新节点 A[i]，并在该节点上记录 A[i] 出现了 1 次，否则就直接找到已经存在的 A[i]节点并将其出现次数加 1。因为整数序列 A 是随机的，所以最终所有的 A[i] 会比较均匀地分散在各个表头之后，整个算法的复杂度可以近似达到 O(n)。

例题 Snowflake Snow Snowflakes

雪花上有 6 个数形成环状，只有当从某个位置为起点，按顺时针或逆时针，能完全和另一个雪花相同时，判断为有两个相同的雪花。现有 n 片雪花，判断是否存在两片相同的雪花。

const int SIZE = 100010;
int n, tot, P = 99991, snow[SIZE][6], head[SIZE], next[SIZE];
int H(int *a) {
    int sum = 0, mul = 1;
    for(int i = 0;i < 6;i ++) {
        sum = (sun + a[i]) % P;
        mul = (long long) mul * a[i] % P;
    }
    return (sum + mul) % P;
}

bool equal(int *a, int *b) {
    for(int i = 0;i < 6;i ++) {
        for(int j = 0;j < 6;j ++) {
            bool eq = 1;
            for(int k = 0;k < 6;k ++) {
                if(a[(i + k) % 6] != b[(j + k) % 6]) eq = 0;
            }
            if(eq) return 1;
            for(int k = 0;k < 6;k ++{
                if(a[(i + k) % 6] != b[(j - k + 6) % 6]) eq = 0;
            }
            if(eq) return 1;
        }
    }
    return 0;
}

bool insert(int *a) {
    int val = H(a);
    for(int i = head[val];i;i = next[i]) {
        if(equal(snow[i], a)) return 1;
    }
    ++ tot;
    memcpy(sonw[tot], a, 6 * sizeof(int));
    next[tot] = head[val];
    head[val] = tot;
    return 0;
}

int main() {
    cin >> n;
    for(int i = 1;i <= n;i ++){
        int a[10];
        for(int j = 0;j < 6;j ++) cin >> a[j];
        if(insert(a)) {
            cout << "Twin snowflakes found." << endl;
            return 0;
        }
    }
    cout << "No two snowflakes are alike." << endl;
    return 0;
}

字符串Hash

字符串 Hash 可以将一个任意长度的字符串映射成一个非负整数，并且其冲突概率几乎为零。
取一固定值 P，把字符串看成 P 进制数，并分配一个大于 0 的数值，代表每种字符。一般来说，我们分配的数值远小于 P。例如对于小写字母构成的字符串，可以令 a = 1,b = 2,···,z = 26。取一固定值 M，求出该 P 进制数对 M 的余数，作为该字符串的 Hash 值。
一般来说，我们取 P = 131 或 P = 13331，此时 Hash 值产生冲突的概率极低，只要 Hash 值相同，我们就可以认为原字符串是相等的。通常我们取 M = 2⁶⁴，即直接使用 unsighed long long 类型来存储这个 Hash 值，在计算时不处理算术溢出问题，产生溢出相当于自动对 2⁶⁴ 取模，这样可以避免低效的取模 (mod) 运算。
如果我们已知字符串 S 的 Hash 值为 H(S)，那么在 S 后添加一个字符 c 构成新的字符串 S + c 的 Hash 值就是 H(S + c) = (H(S) * P + value[c]) mod M。其中乘 P 就相当于 P 进制下的左移运算，value[c] 是我们为 c 选定的代表数值。
如果我们已知字符串 S 的 Hash 值为 H(S)，字符串 S + T 的 Hash 值为 H(S + T)，那么字符串 T 的 Hash 值 H(T) = (H(S + T) - H(S) * P^length(T)) mod M。

我们可以通过 O(N) 的时间预处理字符串所有前缀 Hash 值，并在 O(1) 的时间内查询它任意字串的 Hash 值。

例题 兔子与兔子

很久很久以前，森林里住着一群兔子。
有一天，兔子们想要研究自己的 DNA 序列。
我们首先选取一个好长好长的 DNA 序列（小兔子是外星生物，DNA 序列可能包含 26个小写英文字母）。
然后我们每次选择两个区间，询问如果用两个区间里的 DNA 序列分别生产出来两只兔子，这两个兔子是否一模一样。
注意两个兔子一模一样只可能是他们的 DNA 序列一模一样。
1≤length(S),m≤1000000

char s[1000010];
unsigned long long f[1000010], p[1000010];
int main() {
    scanf("%s", s + 1);
    int n = strlen(s + 1), q;
    cin >> q;
    p[0] = 1;
    for(int i = 1;i <= n;i ++) {
        f[i] = f[i - 1] * 131 + (s[i] - 'a' + 1);
        p[i] = p[i - 1] * 131;
    }
    for(int i = 1;i <= q;i ++) {
        int l1, l2 ,r1, r2;
        cin >> l1 >> l2 >> r1 >> r2;
        if(f[r1] - f[l1 - 1] * p[r1 - l1 + 1] == f[r2] - f[l2 - 1] * p[r2 - l2 + 1]) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
}

---

树状数组

树状数组是一种支持单点修改和区间查询的，代码量小的数据结构。
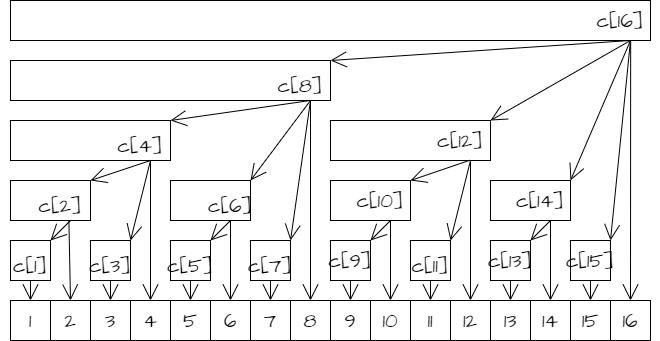
树状数组的基本用途是维护序列的前缀和，对于给定的序列 a，我们建立一个数组 c，其中 c[x] 保存序列 a 的区间 [x - lowbit(x) + 1, x] 中所有数的和。
事实上，数组c可看作如下图的一个树形结构。最下面一行的 N 个叶节点 (N = 16)，代表数值 a[1~N]。该结构满足以下性质：

1. 每个内部节点 c[x] 保存以它为根的子树中所有叶节点的和；
2. 每个内部节点 c[x] 的子节点个数等于 lowbit(x) 的位数；
3. 除树根外，每个内部节点 c[x] 的父节点是 c[x + lowbit(x)]；
4. 树的深度为 O(log N)；
   如果 N 不是 2 的整次幂，那么树状数组是一个具有同样性质的森林结构。
   

区间查询

未完待续